[ADsP 미어캣 온라인 스터디 11기] Day 15

 

 

• subset(data, 조건) : 데이터 프레임 data에서 조건을 만족하는 행만 선택하는 함수입니다.
• 여기서 iris 데이터셋에서 Species(붓꽃의 종류)가 'setosa' 또는 'versicolor'인 행을 선택합니다.
• iris_bin1 데이터에서 Species(꽃의 종) 변수는 범주형(Factor) 변수로 저장됩니다.
• 보통 R에서는 Factor 변수가 자동으로 1, 2, 3 등의 숫자로 인코딩됩니다:
  • setosa → 1
  • versicolor → 2

 

 

 

 

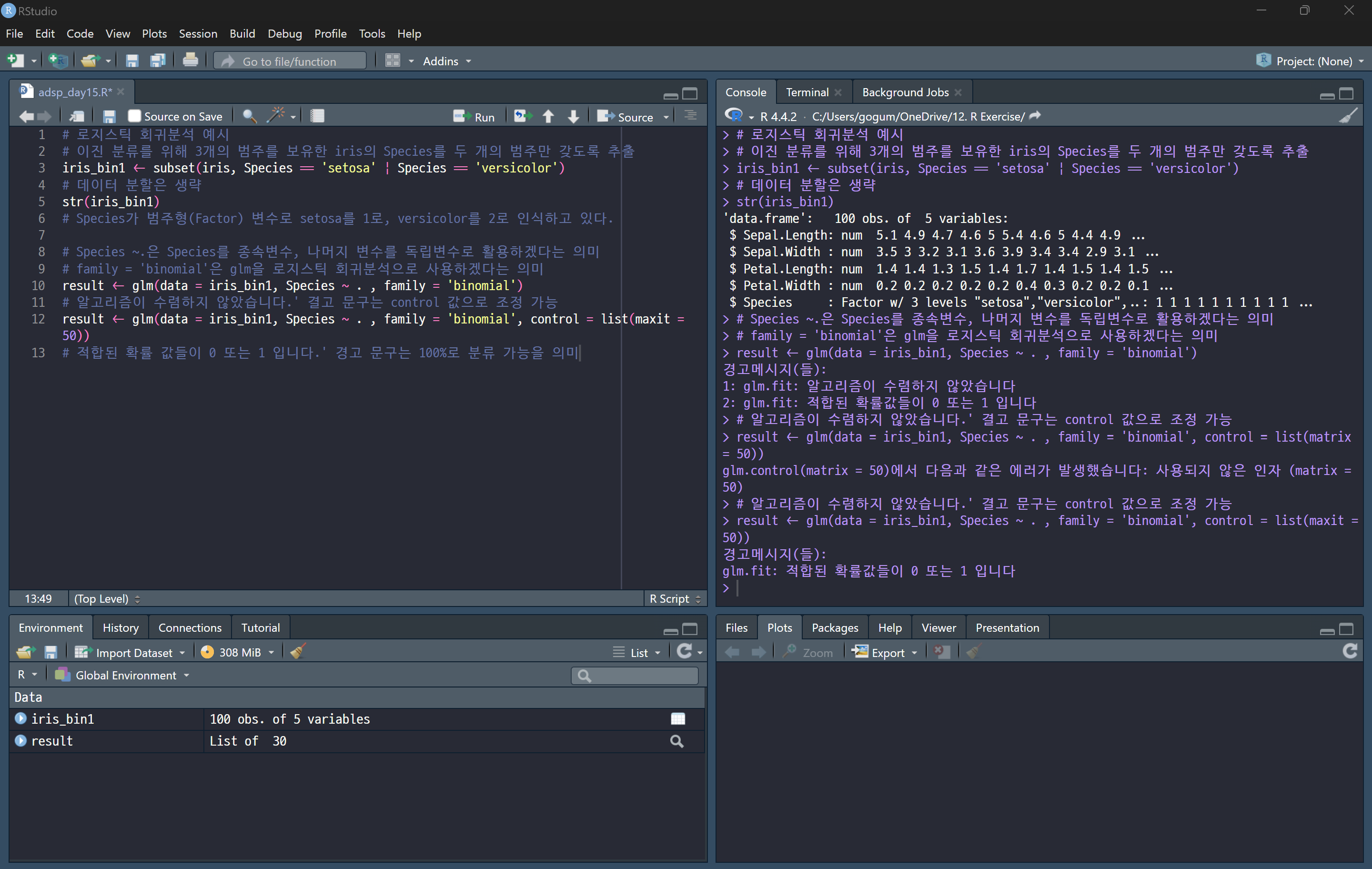
glm() 함수: 일반화 선형 모델 (Generalized Linear Model)

glm() 함수는 **일반화 선형 모델(Generalized Linear Model, GLM)**을 만드는 함수로, 로지스틱 회귀, 포아송 회귀 등 다양한 회귀 모델을 구축할 때 사용됩니다.

📌 glm() 수렴 문제 해결

모델 학습 시 "알고리즘이 수렴하지 않았습니다." 라는 오류가 발생할 수 있음.

✅ 해결 방법: control 매개변수 설정

 

• maxit = 50: 최대 반복 횟수를 50회로 설정 (기본값: 25)
• 일반적으로 데이터가 선형적으로 분리되지 않을 때 발생하는 문제.
• maxit 값을 늘리면 경사 하강법(Gradient Descent)이 더 많은 반복을 수행하여 수렴할 가능성이 높아짐.

 

📌 0 또는 1 확률 출력 경고 해결

🚨 경고 메시지: "적합된 확률 값들이 0 또는 1 입니다."

• 이는 데이터가 완벽하게 분리(Pure Separation) 되는 경우 발생.
• 즉, 모델이 100% 정확도로 분류 가능할 때 나타남.
• 일반적으로 로지스틱 회귀에서 과적합(Overfitting) 가능성을 시사.

 

 

 

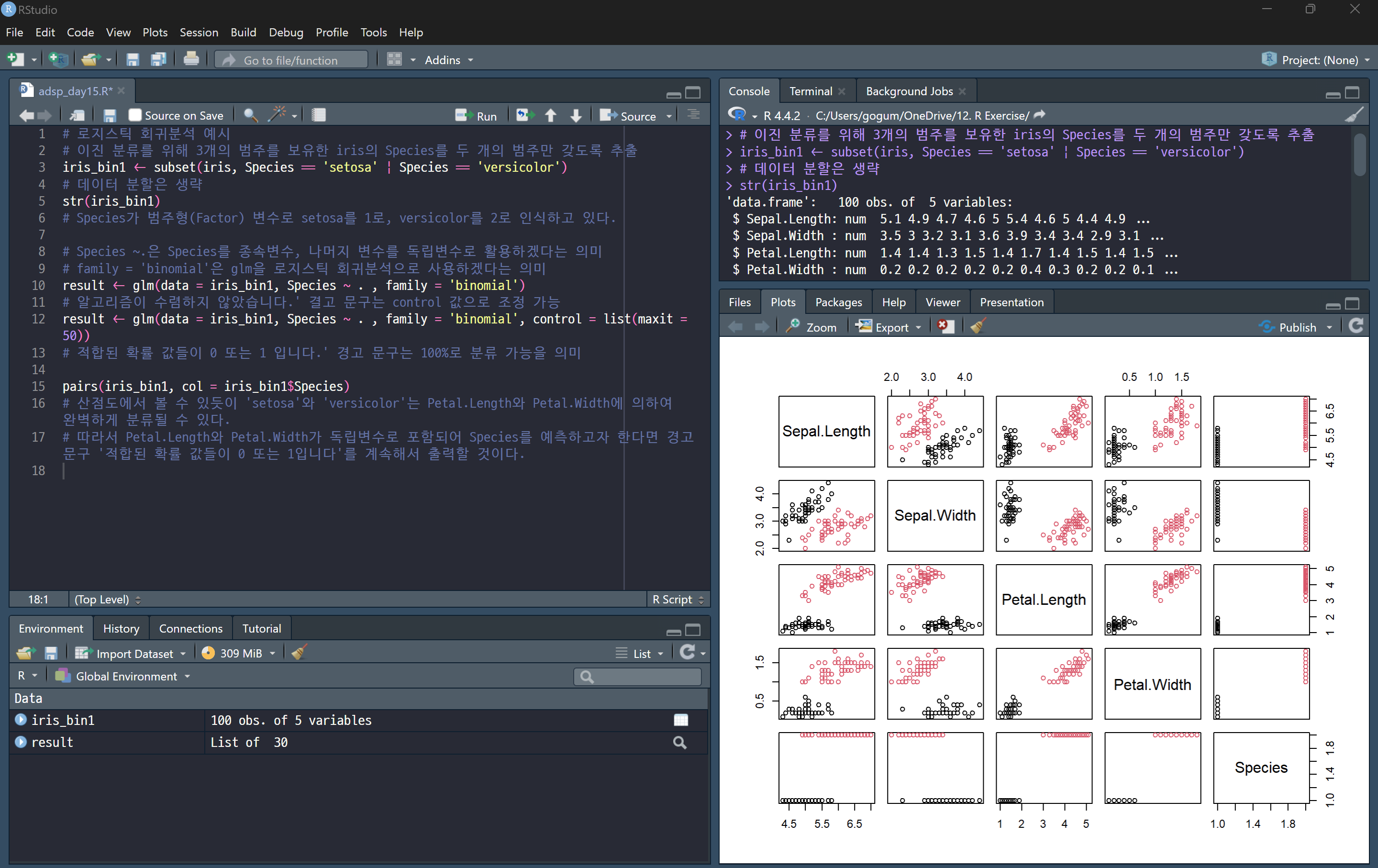
col = iris_bin1$Species → Species에 따라 점의 색상을 다르게 지정함.

예를 들어, setosa는 빨강, versicolor는 파랑으로 표시될 수 있음.

 

📌 그래프 해석 방법

1️⃣ 대각선 (Diagonal)

• 대각선에는 보통 각 변수의 히스토그램 또는 변수명이 표시됨.
• 변수의 분포를 확인할 수 있음.

2️⃣ 변수 간 관계 (Off-Diagonal)

• 각 변수 쌍에 대한 산점도가 표시됨.
• x축은 해당 열의 변수, y축은 해당 행의 변수.
• 두 변수가 선형 관계를 보이면 회귀 분석에 유리.

3️⃣ 종 (Species)에 따른 분포

• 색상별로 데이터가 구분되는지 확인.
• 만약 두 범주(Species)가 완전히 분리된다면, 해당 변수는 종 분류에 매우 유용한 특징(Feature).
• 만약 완전히 겹친다면, 이 변수는 분류에 큰 도움이 되지 않음.

 

Species는 범주형(Factor) 변수이며, pairs() 함수는 수치형 변수들 간의 관계를 나타내는 산점도 행렬을 생성하기 때문에 Species 자체는 그래프에 포함되지 않습니다. 하지만 col = iris_bin1$Species를 설정했기 때문에, 각 점의 색깔이 Species에 따라 다르게 표시됩니다.

 

 

 

 

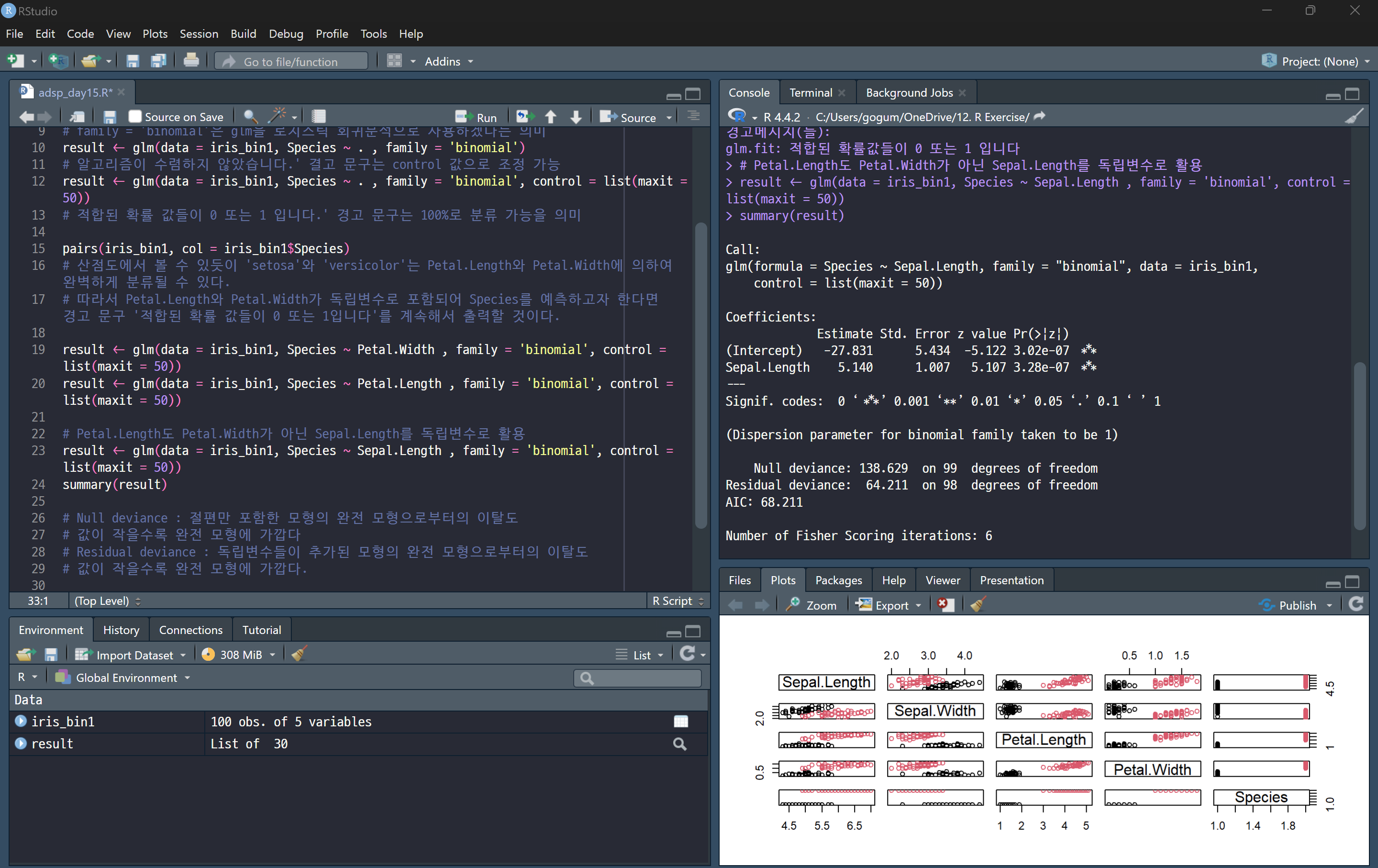
• Null deviance (138.629)
  → 독립변수를 사용하지 않고, 기본 평균값만 사용할 경우의 모델 오차
• Residual deviance (64.211)
  → Sepal.Length 변수를 추가한 후의 모델 오차
  → 값이 작을수록 모델이 데이터를 더 잘 설명
• deviance 차이 (138.629 - 64.211 ≈ 74.418) → 감소! ✅
  → 즉, Sepal.Length 변수를 추가하니 모델이 훨씬 좋아짐 🎯
• AIC (Akaike Information Criterion, 68.211)
  → 모델의 적합도를 평가하는 기준 (낮을수록 좋은 모델)
• "Fisher Scoring iterations: 6"
  → 최적의 계수를 찾기 위해 6번 반복
  → 정상적으로 수렴했으므로 문제 없음 ✅

 

 

 

 

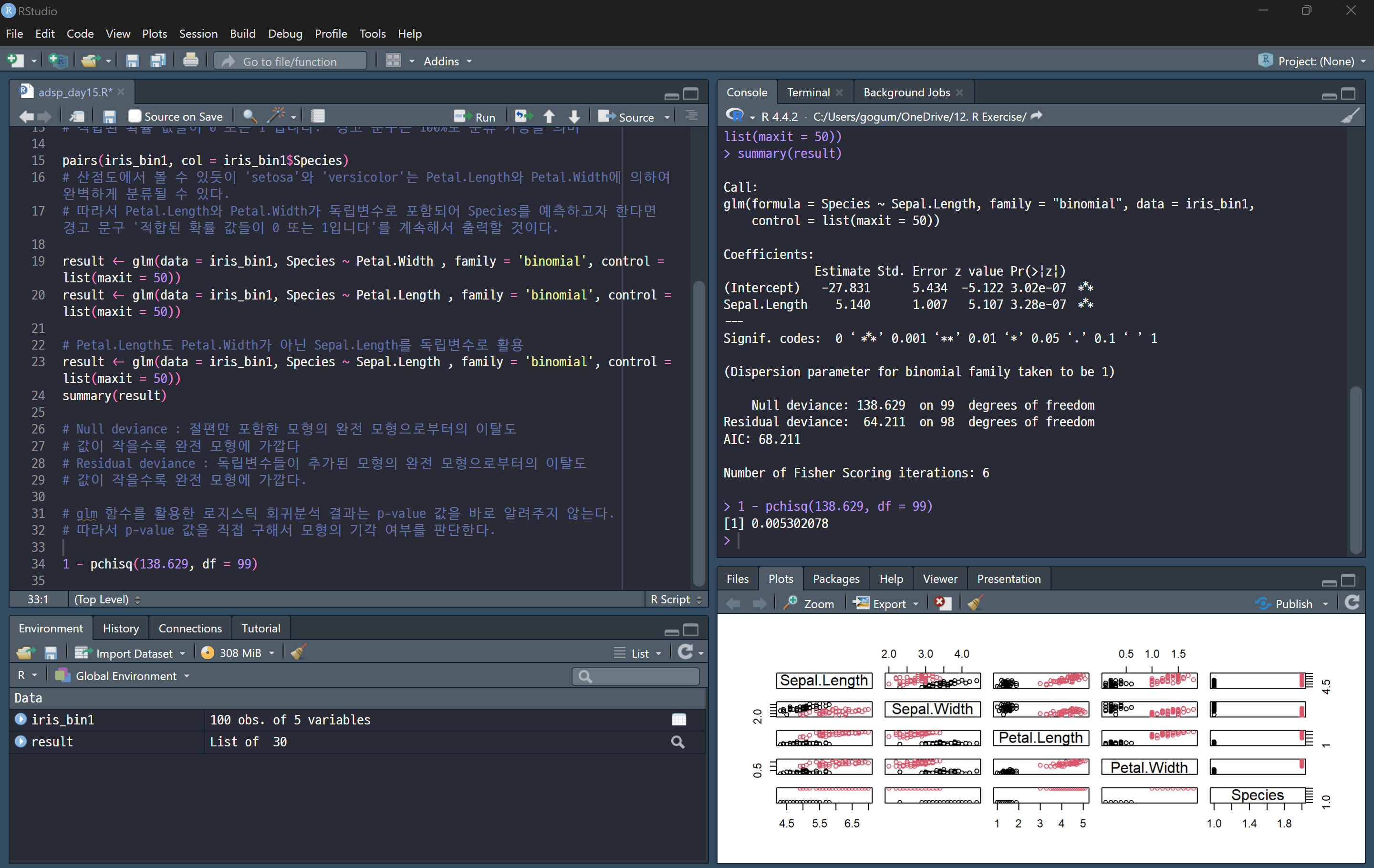
glm 함수의 로지스틱 회귀 분석 결과에서는 p-value 값을 직접적으로 제공하지 않는 이유는 모델에 대한 가설 검정이 두 가지 중요한 방법을 사용할 수 있기 때문입니다. 첫 번째 방법은 회귀 계수에 대한 유의성 검정이고, 두 번째는 모델의 적합도를 평가하는 검정입니다. glm 함수는 회귀 계수에 대한 유의성 검정 결과를 출력하지만, 모델 자체에 대한 적합도 검정 결과는 직접적으로 제공하지 않습니다.

glm 함수에서 바로 제공되지 않는 p-value는 모델의 적합도에 대한 평가 결과입니다. pchisq와 같은 함수를 이용하여 Deviance 값을 기반으로 모델의 적합도에 대한 p-value를 직접 계산해 주어야 합니다.

세부 해석:

1. pchisq(138.629, df = 99):
   pchisq 함수는 카이제곱 분포에 대한 **누적 분포 함수 (CDF)**를 계산합니다. 이 함수는 특정 값(여기서는 138.629)이 **자유도(df)**가 99인 카이제곱 분포에서 나올 확률을 제공합니다. 즉, 138.629보다 작은 값이 나올 확률을 계산하는 것입니다.
   • 138.629: Deviance 값 (이 모델이 가진 적합도)
   • df = 99: 자유도 (이 모델의 자유도, 즉 데이터의 개수에서 추정된 파라미터 수를 뺀 값)
2. 1 - pchisq(...):
   카이제곱 분포에서 특정 값보다 큰 확률을 구하는 것입니다. 따라서 이 부분은 Deviance 값이 138.629보다 클 확률, 즉 모델이 잘 맞지 않을 확률을 나타냅니다.
3. 결과:
   1 - pchisq(138.629, df = 99)의 결과는 모델의 적합도에 대한 p-value로, 이 값이 작으면 모델이 데이터에 잘 맞지 않는다고 판단할 수 있습니다. 일반적으로 p-value가 0.05보다 작으면 모델을 기각하고, 0.05보다 크면 모델이 적합하다고 판단합니다.

 

 

 

 

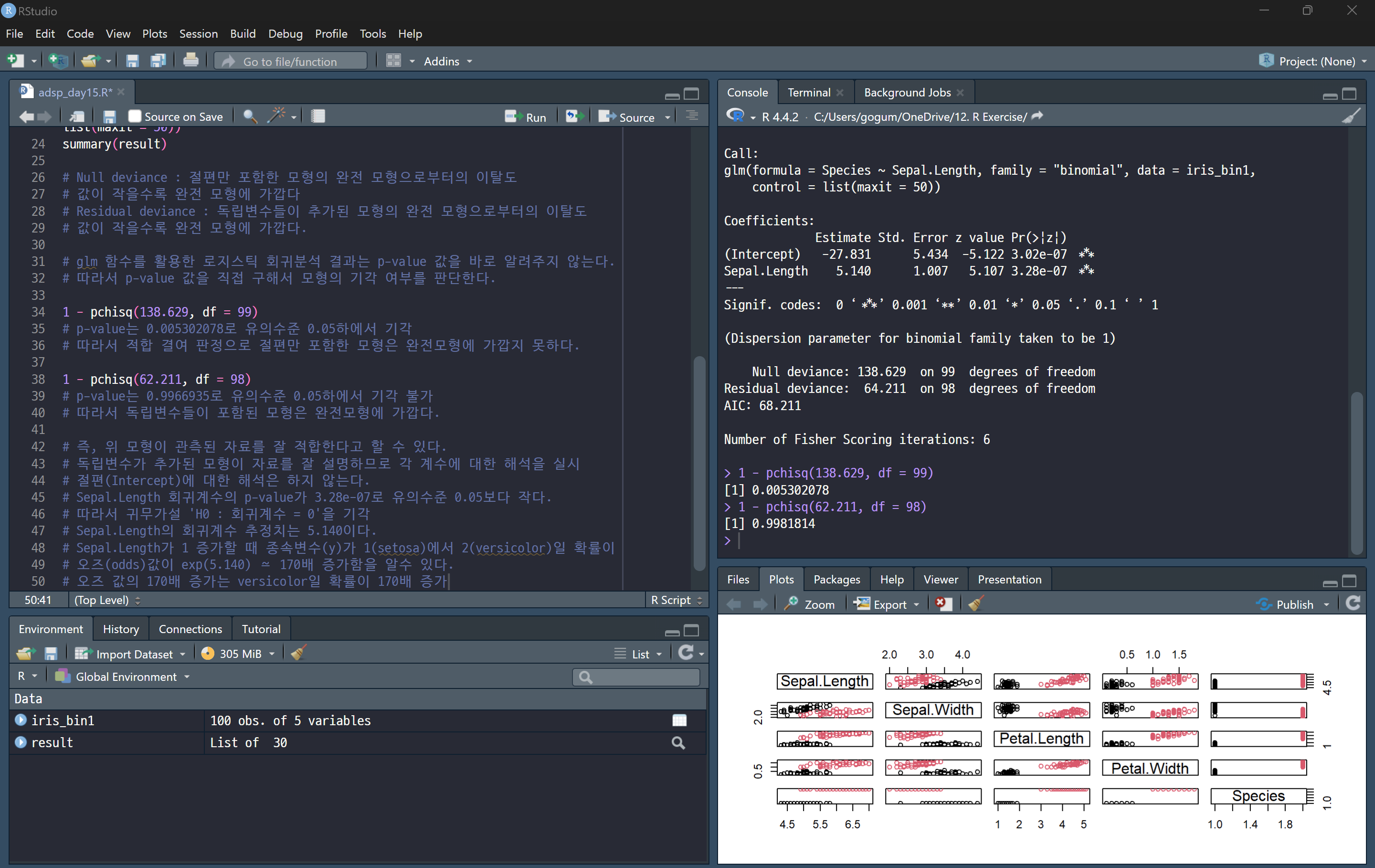
로지스틱 회귀분석에서 **오즈(odds)**와 **오즈비(odds ratio)**는 중요한 개념입니다. 이를 통해 변수의 변화가 종속변수에 미치는 영향을 해석할 수 있습니다.

여기서 Sepal.Length에 대한 회귀계수 5.140을 기준으로 **오즈(odds)**와 **오즈비(odds ratio)**를 어떻게 해석할 수 있는지 차근차근 풀어 보겠습니다.

1. 로지스틱 회귀에서 오즈(odds)란?

로지스틱 회귀에서 종속변수는 이진 변수 (예: setosa 또는 versicolor)입니다. 여기서는 setosa를 1로, versicolor를 2로 두고 있는데, 이 두 범주에 대한 **"확률"**을 구하는 대신 **"오즈(odds)"**를 사용합니다.

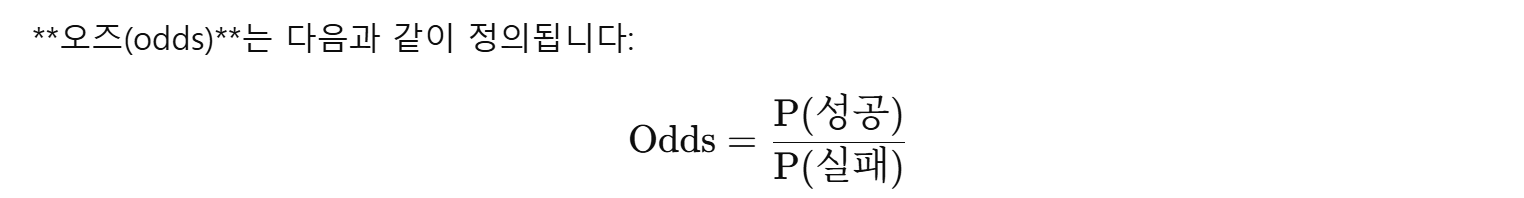
즉, **성공 확률(P(성공))**을 **실패 확률(P(실패))**로 나눈 값입니다. 로지스틱 회귀는 이 **오즈(odds)**의 로그 변환을 다루는데, 이 값을 예측하기 위해 **로지스틱 함수(logit)**를 사용합니다.

2. 회귀계수와 오즈의 관계

로지스틱 회귀에서의 회귀계수 5.140은 Sepal.Length가 1 단위 증가할 때 **log(odds)**가 얼마나 변화하는지를 나타냅니다. 이때 **log(odds)**는 오즈의 로그입니다.

즉, Sepal.Length의 회귀계수 5.140은 Sepal.Length가 1 증가할 때, 오즈의 로그가 5.140만큼 증가한다는 의미입니다.

3. 오즈비(odds ratio)

오즈비는 오즈의 비율을 나타냅니다. 회귀계수의 지수화(exponentiation)를 통해 **오즈비(odds ratio)**를 구할 수 있습니다.

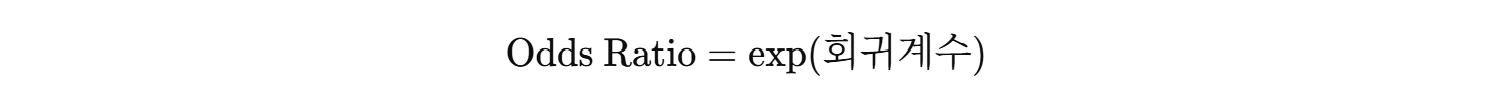
따라서, Sepal.Length의 회귀계수 5.140에 대해 **exp(5.140)**을 계산하면 약 170이 나옵니다. 이것은 Sepal.Length가 1 증가할 때 오즈가 170배 증가한다는 의미입니다.

4. 해석

• Sepal.Length가 1 증가할 때, setosa에서 versicolor로 분류될 확률이 170배 증가한다고 해석할 수 있습니다.
• 즉, Sepal.Length가 1 증가함에 따라 versicolor로 분류될 **오즈(odds)**가 170배 더 높아진다는 것입니다.

 

 

 

 

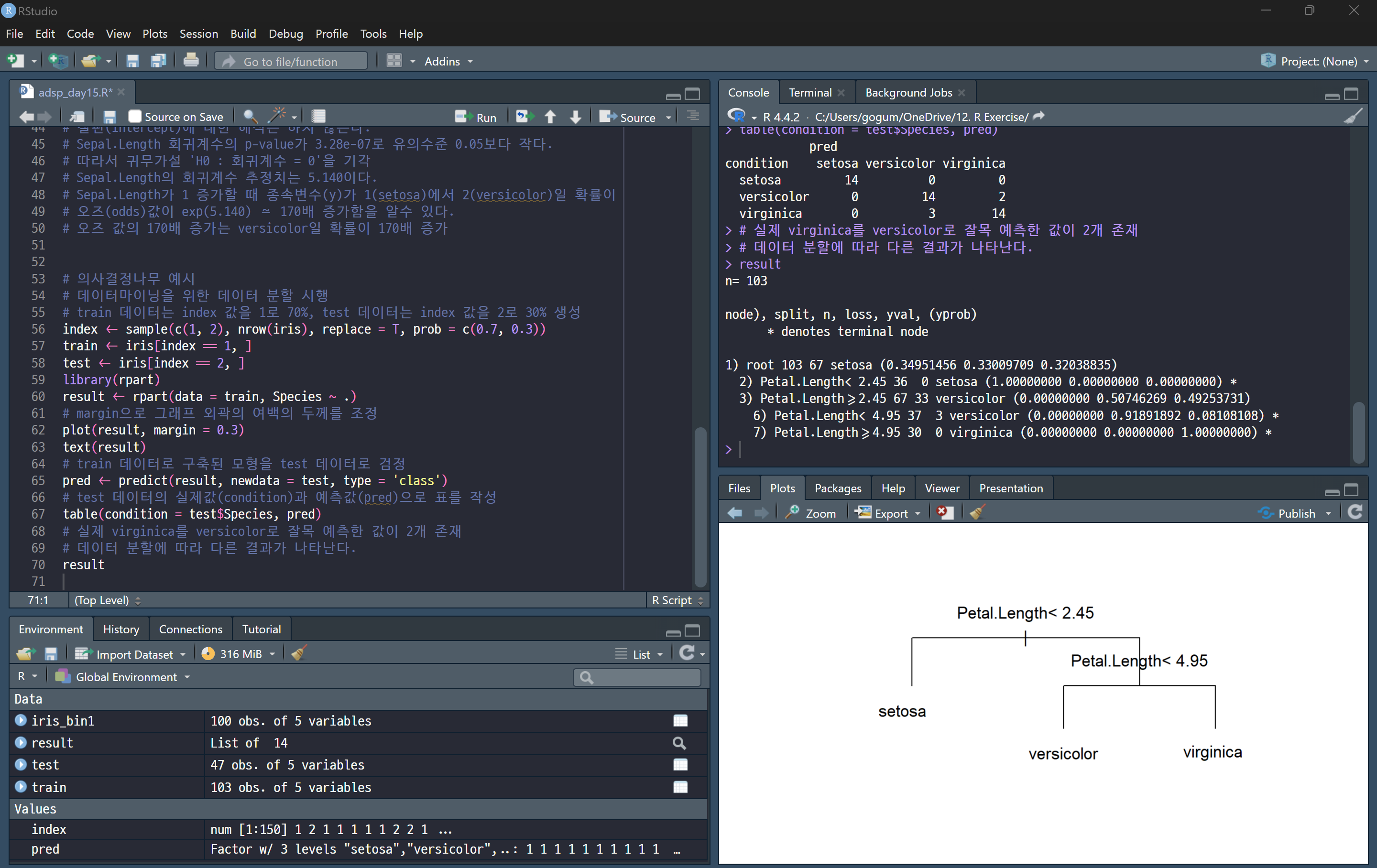
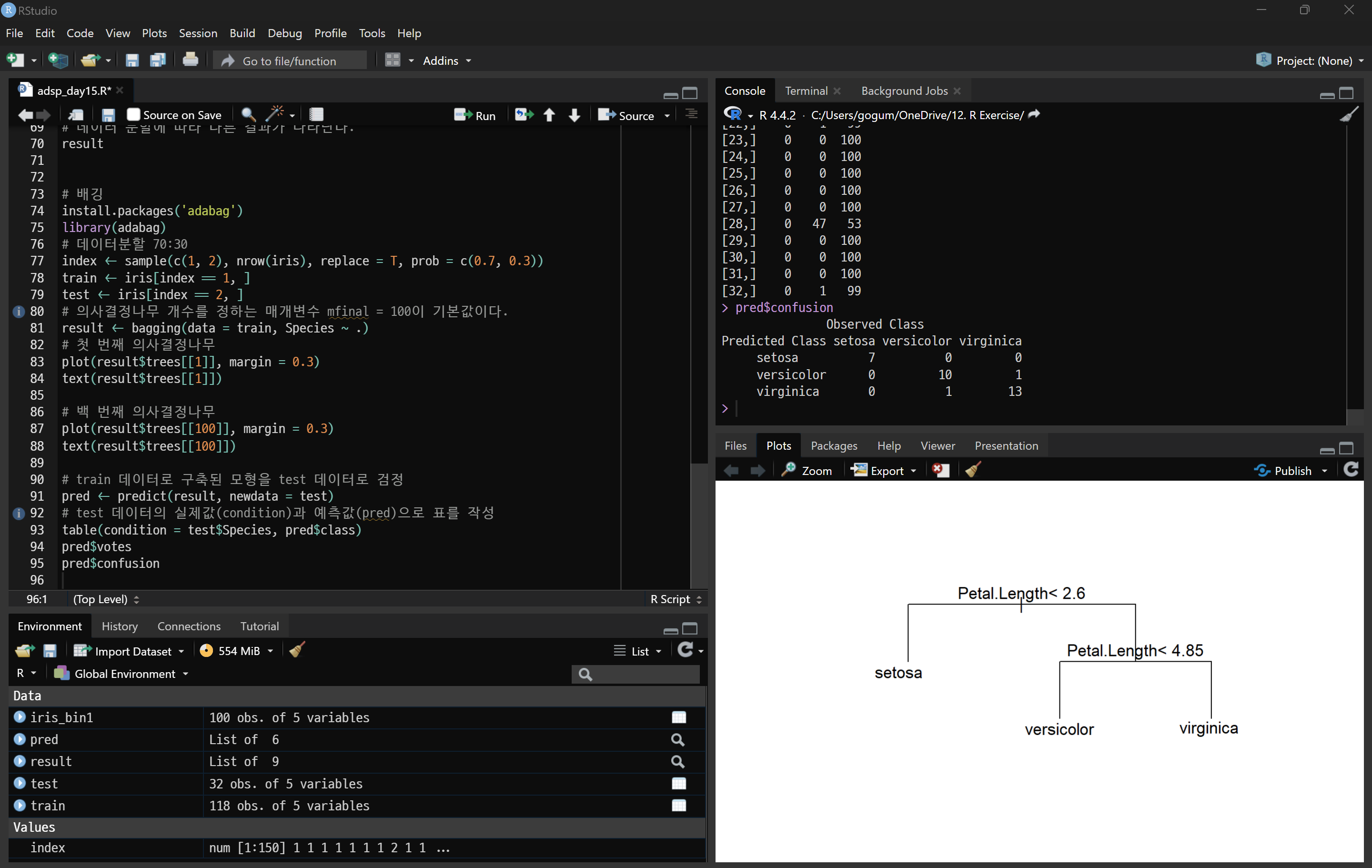
predict(result, newdata = test, type = 'class') : 학습된 모델(result)을 사용하여 **테스트 데이터(test)**에 대해 예측을 수행

• newdata = test: 예측에 사용할 데이터는 test입니다.
• type = 'class': 예측 결과를 클래스(범주) 값으로 반환합니다. 이 경우, Species의 예측 값이 setosa, versicolor, virginica 중 하나로 나옵니다.

 

 

 

 

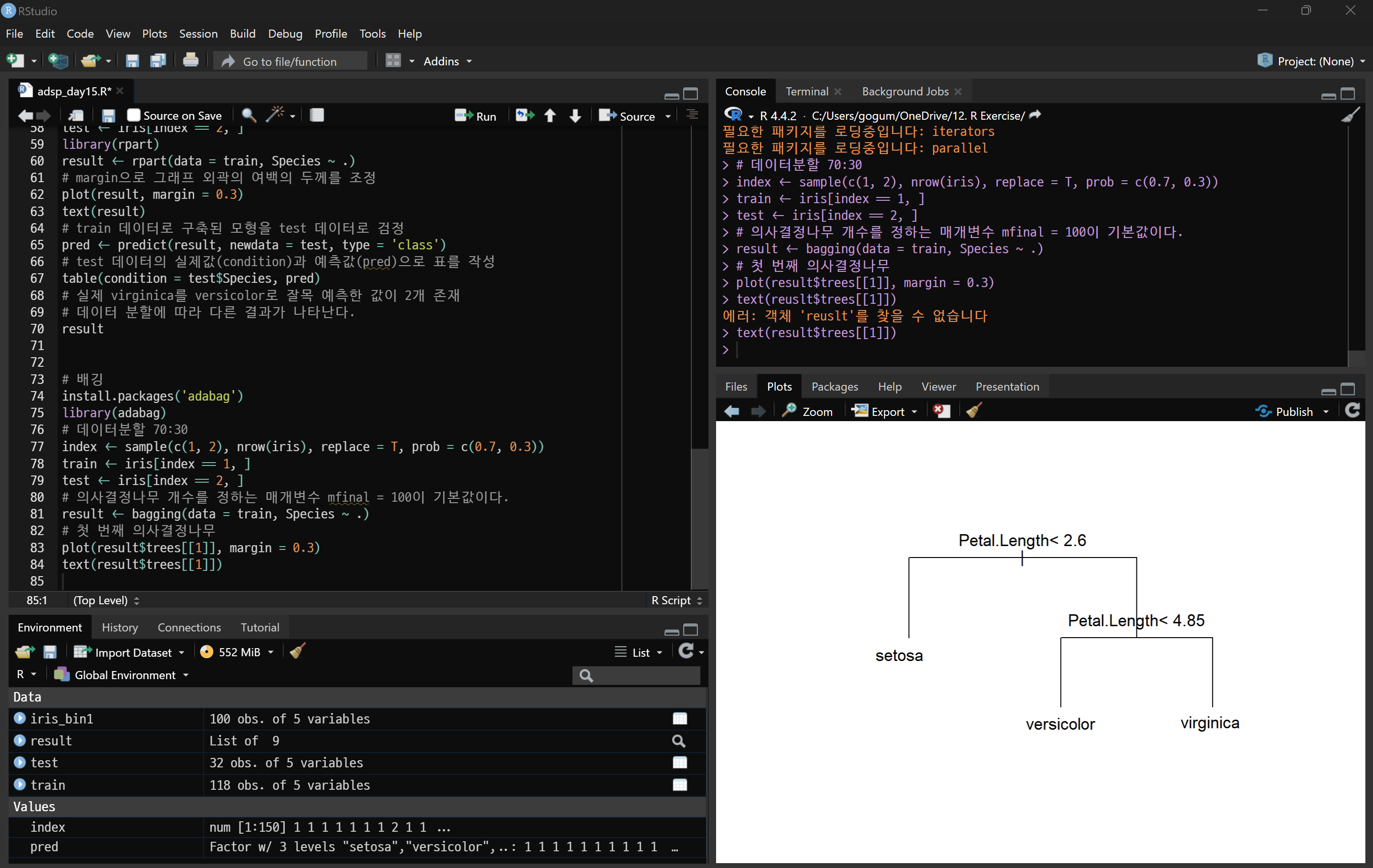
sample(c(1, 2), nrow(iris), replace = T, prob = c(0.7, 0.3)): iris 데이터셋을 70%는 훈련 데이터(train), 30%는 테스트 데이터(test)로 분할합니다.

• replace = T: 복원 추출 방식을 사용하여 각 데이터가 중복될 수 있도록 합니다.
• prob = c(0.7, 0.3): 70%는 훈련 데이터(1), 30%는 테스트 데이터(2)로 할당됩니다.