[ADsP 미어캣 온라인 스터디 11기] Day 11 3과목 회귀분석

회귀분석
하나 이상의 독립변수들이 종속변수에 얼마나 영향을 미치는지 추정
독립변수 1개 : 단순선형회귀분석
독립변수 2개 이상 : 다중선형회귀분석
기본적으로 연속형 변수일 때 사용
범주형일 경우 로지스틱 회귀분석 사용
회귀분석의 종류
| 종류 | 모형 |
| 단순회귀 | 1개의 독립변수와 반응변수가 직선(선형) 관계 |
| 다중회귀 | K개의 독립변수와 반응변수가 선형 관계 |
| 다항회귀 | K개의 독립변수와 반응변수가 2차함수 이상의 관계 |
| 비선형회귀 | 회귀식이 미지의 모수들과 선형관계가 아닌 경우 |
회귀분석의 가정
| 선형성 | 독립변수와 종속변수가 선형적 |
| 독립성 | 단순회귀분석에서 잔차와 독립변수 값이 서로 독립 다중회귀분석의 경우 독립변수들 간에 상관성이 없이 독립 |
| 등분산성 | 잔차의 중심에서 분산이 같아야 한다. |
| 정규성 | 잔차항이 정규분포 형태를 띠는 것 |
단순선형회귀분석
독립변수와 종속변수가 1개씩일 때 둘 사이의 인과관계 분석(선형)
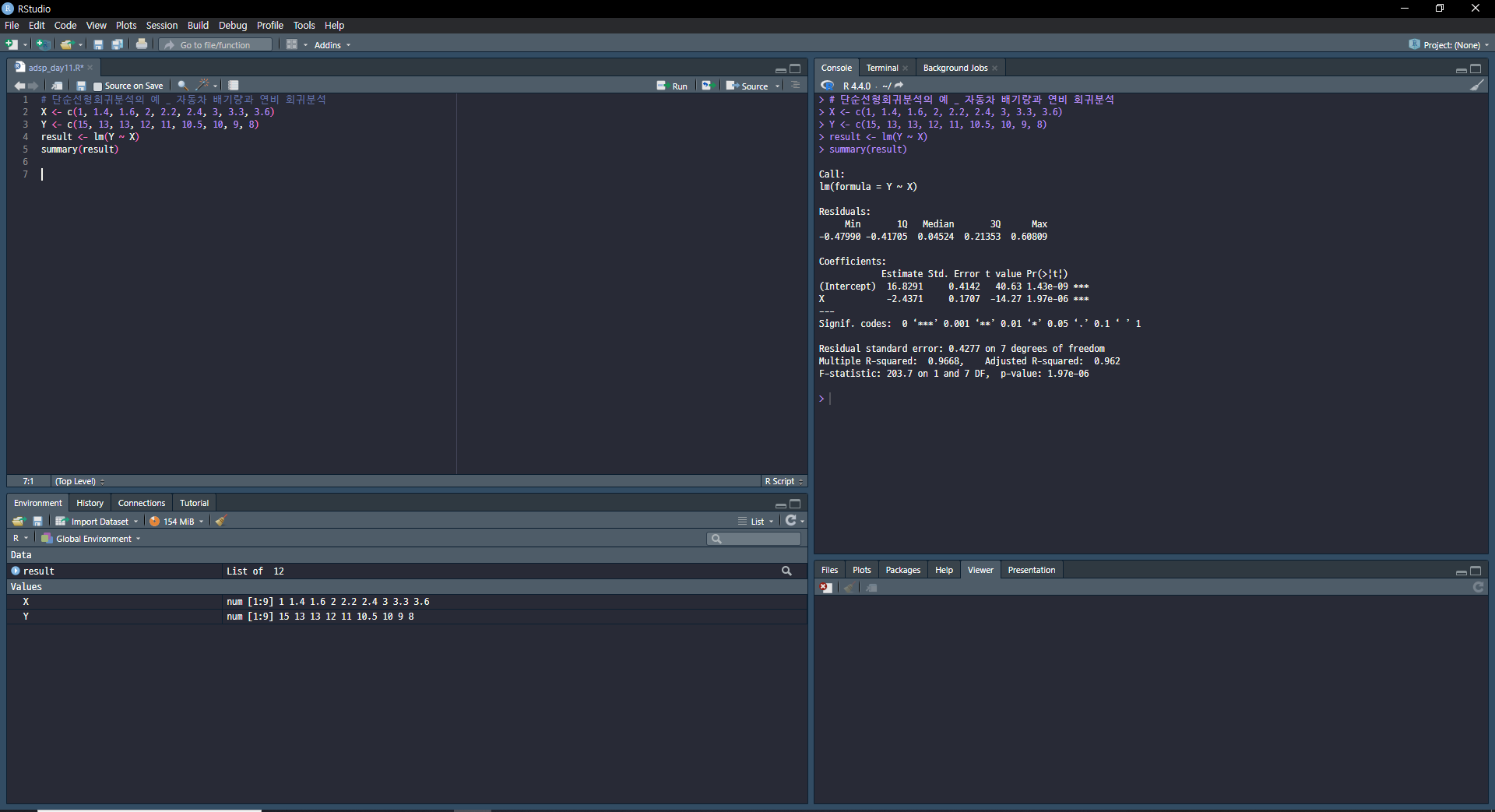
최소제곱법으로 회귀계수 추정
최소제곱법이란 실제 관측치와 추세선에 의해 예측된 점사이의 거리, 즉 오차를 제곱해 더한 값을 최소화하는 것이다.
| SST(총제곱합) | 전체 설명이 필요 |
| SSE(오차제곱합) | 모형이 설명하지 못하는 부분 |
| SSR(회귀제곱합) | 모형이 설명하는 부분 |
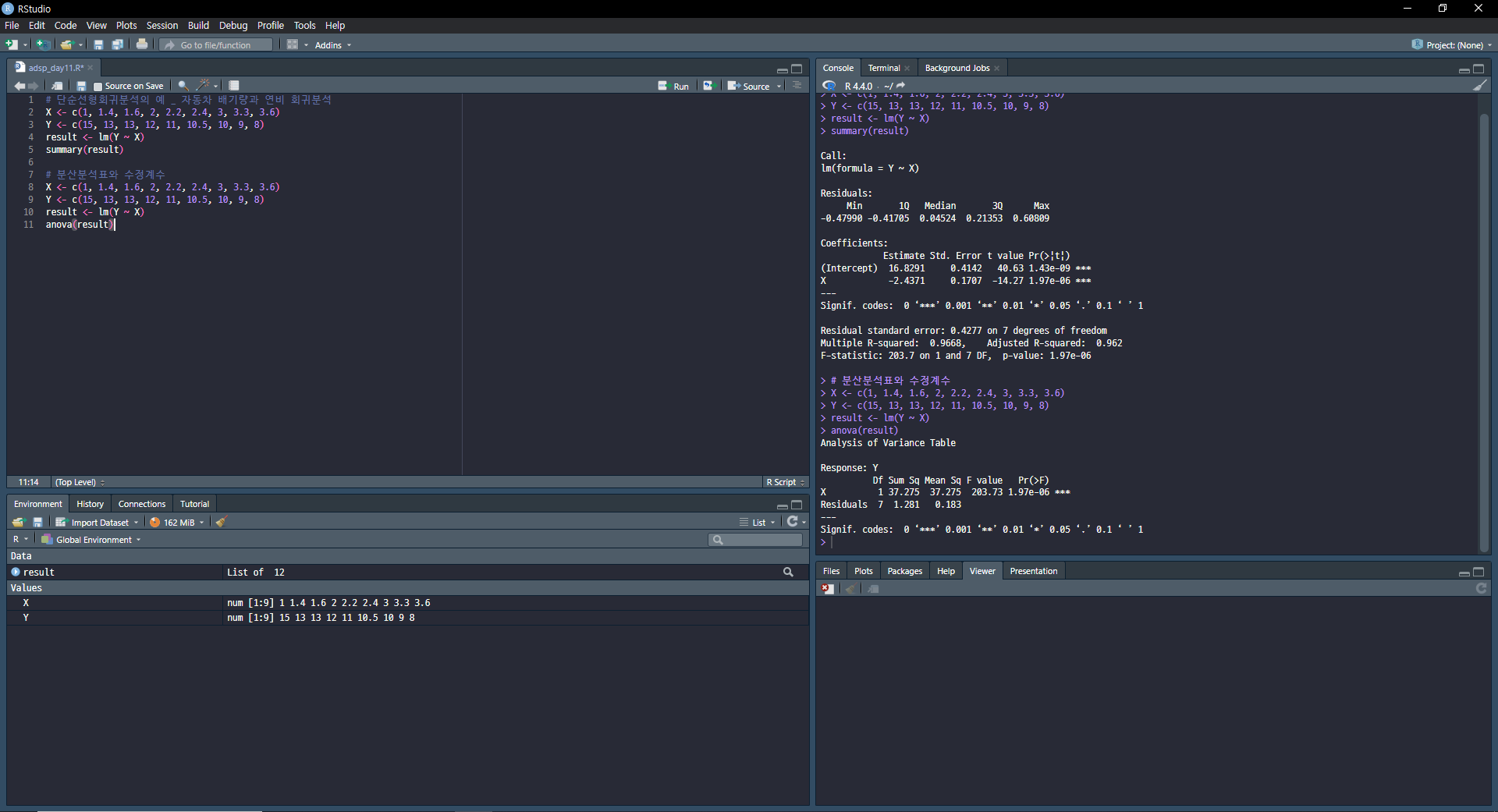
회귀분석모형의 적합성
회귀분석의 결과에 대한 모형 적합성을 검증하기 위해 분산분석표 사용
독립변수가 1개 : 단순회귀분석
독립변수가 2개이상 : 다중회귀분석
회귀모형의 통계적 유의성 검증
F검정을 통해 확인(분산의 차이)
분산의 차이가 크다 = 회귀계수가 크다 = 변수 간에 유의미한 인과관계가 존재한다.
F값이 크면 P값이 작아짐
P값 : F값이 '0'에 얼마나 가까운지 확률적으로 측정한 값
회귀계수의 유의성 검증
t-검정을 통해 확인
t-통계량 : 회귀계수를 표준오차로 나눈 값
t-통계량이 크다 = 표준오차가 작다 = 회귀계수가 커짐 = 유의미한 인과관계 O = P값은 작아짐
모형의 설명력
회귀모형의 설명력이 좋다는 의미는 데이터들의 분포가 회귀선에 밀접하게 분포하고 있다는 의미
회귀분석 결과를 분산분석하고, 도출된 결정계수로 모형의 설명력을 판단
결정계수 = SSR/SST
결정계수가 1에 가깝다면 데이터들이 회귀선에 매우 밀접 -> 예측력이 높다
다중선형회귀분석
독립변수가 2개 이상이고 종속변수가 하나일 때 선형으로 표현
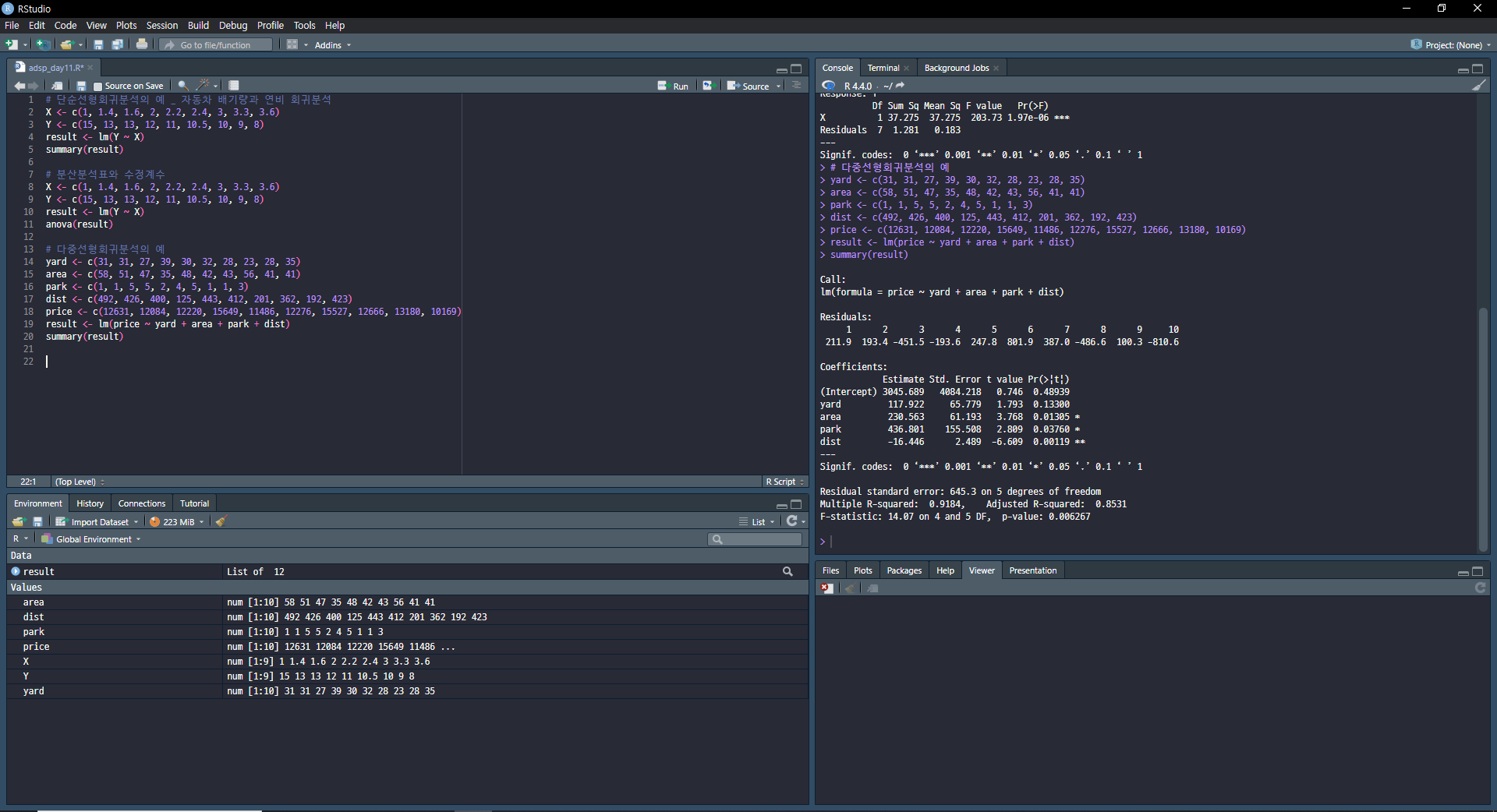
다중공선성
회귀분석에서 독립변수간에 강한 상관관계가 나타나는 문제
결정계수 값은 높지만 P-value값이 커서 개별 인자가 유의하지 않을 경우 의심

분산팽창요인(VIF)가 10을 넘으면 다중공산성이 있다고 판단
최적회귀방정식
1개의 반응변수y를 설명하기 위한 k개의 독립변수 후보들이 있을 때 반응변수 y를 가장 잘 설명할 수 있는 회귀식을 찾는 것
최적의 회귀방정식을 도출하기 위한 방법
1) 부분집합법 = 임베디드 기법
모든 가능한 모델을 고려하여 가장 좋은 모델 선정
라쏘, 릿지, 엘라스틱넷 등
2) 단계적 변수선택법
일정한 단계를 거치면서 변수를 추가하거나 제거하는 방식
| 전진선택법 | 가장 많은 영향을 줄 것으로 판단되는 변수부터 추가 |
| 후진제거법 | 독립변수를 모두 포함하여 가장 적은 영향을 주는 변수부터 제거 |
| 단계선택법 | 전진선택법과 후진제거법 보완 |
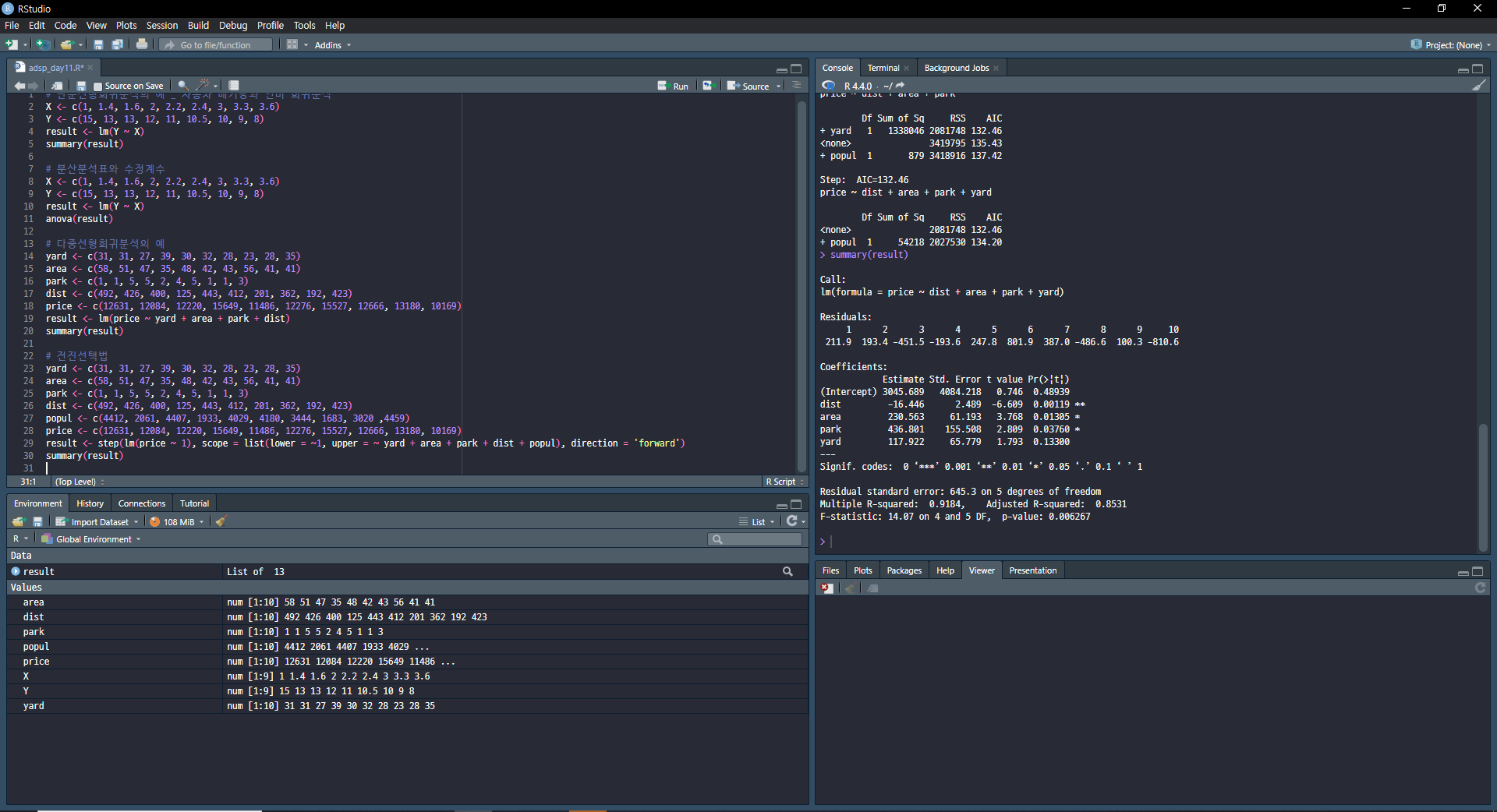
변수 선택에 사용되는 성능지표
별점화 방식의 AIC와 BIC : 변수가 클수록 분산화됨
| AIC | MSE에 변수 수만큼 패널티를 주는 지표 |
| BIC | AIC보다 더 큰 패널티 |
| 멜로우 Cp | 최고자승법 |
정규화 선형회귀
과적합 또는 과대적합 : 모델이 학습 데이터를 과하게 학습하는 것
과적합되면 계수의 크기도 과도하게 증가하는 경향이 있어 이를 방지하기 위해 계수릐 크기를 제한하는 방법을 사용하는데, 이것을 정규화 선형회귀라 부른다.
정규화 선형회귀의 종류
| 라쏘 | L1규제, 가중치들의 절댓값의 합을 최소화하는 것을 제약조건으로 추가 가중치 파라미터를 0으로 만들어 제외시킴 |
| 릿지 | L2규제, 가중치들의 제곱합을 최소화하는 것을 제약조건으로 추가 가중치 파라미터를 0에 가깝게 만들어 제외시김 |
| 엘라스틱넷 | 라쏘와 릿지 결합 |
일반화 선형회귀
회귀분석을 하고 싶지만 종속변수가 범주형 자료이거나 정규성을 만족하지 못하는 경우 그 종속변수를 적절한 함수 f(x)로 정의한 다음, 이함수과 독립변수를 선형 결합하여 회귀분석을 수행할 수 있는데 이를 일반화 선형회귀라 한다.
일반화 선형회귀의 종류
| 로지스틱 회귀 | 종속변수가 범주형 변수(0 or 1)일때 사용 |
| 포아송 회귀 | 특정 시간 동안 발생한 사건의 건수에 대한 도수 자료 |
더빈 왓슨 검정
오차항이 상관관계를 갖는 경우는 대부분 시계열 데이터의 경우
회귀분석시 오차항이 서로 연관성이 없어야 한다.
오차항의 공분산 = 0
0(양의 상관관계) <<< 2(상관관계X) <<< 4(음의 상관관계)